footballfullpac

1. The Complexity Of Nonuniform Random Number Generation Pdf Reader Pdf

Abstract—For numerous computationally complex applica- tions, like financial modelling and Monte Carlo simulations, the fast generation of high quality non-uniform random numbers. (RNs) is essential. The implementation of such generators in. FPGA-based accelerators has therefore become a very active research field. May 18, 2016  None of them say if any language is already supporting non-uniform random number generator. – applefreak Mar 18 '11 at 13:45 C# doesn't support random-number generation at all, it's the BCL that offers it.

A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG),^[1] is an algorithm for generating a sequence of numbers whose properties approximate the properties of sequences of random numbers. The PRNG-generated sequence is not truly random, because it is completely determined by an initial value, called the PRNG's seed (which may include truly random values). Although sequences that are closer to truly random can be generated using hardware random number generators, pseudorandom number generators are important in practice for their speed in number generation and their reproducibility.^[2]

PRNGs are central in applications such as simulations (e.g. for the Monte Carlo method), electronic games (e.g. for procedural generation), and cryptography. Cryptographic applications require the output not to be predictable from earlier outputs, and more elaborate algorithms, which do not inherit the linearity of simpler PRNGs, are needed.

Good statistical properties are a central requirement for the output of a PRNG. In general, careful mathematical analysis is required to have any confidence that a PRNG generates numbers that are sufficiently close to random to suit the intended use. John von Neumann cautioned about the misinterpretation of a PRNG as a truly random generator, and joked that 'Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin.'^[3]

Potential problems with deterministic generators[edit]

In practice, the output from many common PRNGs exhibit artifacts that cause them to fail statistical pattern-detection tests. These include:

• Shorter than expected periods for some seed states (such seed states may be called 'weak' in this context);
• Lack of uniformity of distribution for large quantities of generated numbers;
• Correlation of successive values;
• Poor dimensional distribution of the output sequence;
• The distances between where certain values occur are distributed differently from those in a random sequence distribution.

Defects exhibited by flawed PRNGs range from unnoticeable (and unknown) to very obvious. An example was the RANDU random number algorithm used for decades on mainframe computers. It was seriously flawed, but its inadequacy went undetected for a very long time.

In many fields, much research work prior to the 21st century that relied on random selection or on Monte Carlo simulations, or in other ways relied on PRNGs, is much less reliable than it might have been as a result of using poor-quality PRNGs.^[4] Even today, caution is sometimes required, as illustrated by the following warning, which is given in the International Encyclopedia of Statistical Science (2010).^[5]

The list of widely used generators that should be discarded is much longer [than the list of good generators]. Do not trust blindly the software vendors. Check the default RNG of your favorite software and be ready to replace it if needed. This last recommendation has been made over and over again over the past 40 years. Perhaps amazingly, it remains as relevant today as it was 40 years ago.

As an illustration, consider the widely used programming language Java. As of 2017, Java still relies on a linear congruential generator (LCG) for its PRNG;^[6][7] yet LCGs are of low quality—see further below.

The first PRNG to avoid major problems and still run fairly quickly was the Mersenne Twister (discussed below), which was published in 1998. Other high-quality PRNGs have since been developed.

Generators based on linear recurrences[edit]

In the second half of the 20th century, the standard class of algorithms used for PRNGs comprised linear congruential generators. The quality of LCGs was known to be inadequate, but better methods were unavailable. Press et al. (2007) described the result thus: 'If all scientific papers whose results are in doubt because of [LCGs and related] were to disappear from library shelves, there would be a gap on each shelf about as big as your fist'.^[8]

A major advance in the construction of pseudorandom generators was the introduction of techniques based on linear recurrences on the two-element field; such generators are related to linear feedback shift registers.

The 1997 invention of the Mersenne Twister,^[9] in particular, avoided many of the problems with earlier generators. The Mersenne Twister has a period of 2¹⁹⁹³⁷−1 iterations (≈4.3×10⁶⁰⁰¹), is proven to be equidistributed in (up to) 623 dimensions (for 32-bit values), and at the time of its introduction was running faster than other statistically reasonable generators.

In 2003, George Marsaglia introduced the family of xorshift generators,^[10] again based on a linear recurrence. Such generators are extremely fast and, combined with a nonlinear operation, they pass strong statistical tests.^[11][12][13]

In 2006 the WELL family of generators was developed.^[14] The WELL generators in some ways improves on the quality of the Mersenne Twister—which has a too-large state space and a very slow recovery from state spaces with a large number of zeros.

Cryptographically secure pseudorandom number generators[edit]

A PRNG suitable for cryptographic applications is called a cryptographically secure PRNG (CSPRNG). A requirement for a CSPRNG is that an adversary not knowing the seed has only negligibleadvantage in distinguishing the generator's output sequence from a random sequence. In other words, while a PRNG is only required to pass certain statistical tests, a CSPRNG must pass all statistical tests that are restricted to polynomial time in the size of the seed. Though a proof of this property is beyond the current state of the art of computational complexity theory, strong evidence may be provided by reducing the CSPRNG to a problem that is assumed to be hard, such as integer factorization.^[15] In general, years of review may be required before an algorithm can be certified as a CSPRNG.

Some classes of CSPRNGs include the following:

• block ciphers running in counter^[16] or output feedback mode
• PRNGs that have been designed specifically to be cryptographically secure, such as Microsoft's Cryptographic Application Programming Interface function CryptGenRandom, the Yarrow algorithm (incorporated in Mac OS X and FreeBSD), and Fortuna
• combination PRNGs which attempt to combine several PRNG primitive algorithms with the goal of removing any detectable non-randomness
• special designs based on mathematical hardness assumptions – Examples include the Micali–Schnorr generator,^[17]Naor-Reingold pseudorandom function and the Blum Blum Shub algorithm, which provide a strong security proof. Such algorithms are rather slow compared to traditional constructions, and impractical for many applications.
• generic PRNGs - It has been shown that a (cryptographically) secure PRNG can be constructed generically from any one-way function.^[18] However, this generic construction is extremely slow in practice, and is mainly of theoretical interest.

It has been shown to be likely that the NSA has inserted an asymmetric backdoor into the NIST certified pseudorandom number generator Dual_EC_DRBG.^[19]

Most PRNG algorithms produce sequences which are uniformly distributed by any of several tests. It is an open question, and one central to the theory and practice of cryptography, whether there is any way to distinguish the output of a high-quality PRNG from a truly random sequence. In this setting, the distinguisher knows that either the known PRNG algorithm was used (but not the state with which it was initialized) or a truly random algorithm was used, and has to distinguish between the two.^[20] The security of most cryptographic algorithms and protocols using PRNGs is based on the assumption that it is infeasible to distinguish use of a suitable PRNG from use of a truly random sequence. The simplest examples of this dependency are stream ciphers, which (most often) work by exclusive or-ing the plaintext of a message with the output of a PRNG, producing ciphertext. The design of cryptographically adequate PRNGs is extremely difficult, because they must meet additional criteria. The size of its period is an important factor in the cryptographic suitability of a PRNG, but not the only one.

BSI evaluation criteria[edit]

The German Federal Office for Information Security (Bundesamt für Sicherheit in der Informationstechnik, BSI) has established four criteria for quality of deterministic random number generators.^[21] They are summarized here:

• K1 – There should be a high probability that generated sequences of random numbers are different from each other.
• K2 – A sequence of numbers which is indistinguishable from 'true random' numbers according to specified statistical tests. The tests are the monobit test (equal numbers of ones and zeros in the sequence), poker test (a special instance of the chi-squared test), runs test (counts the frequency of runs of various lengths), longruns test (checks whether there exists any run of length 34 or greater in 20 000 bits of the sequence)—both from BSI^[21] and NIST,^[22] and the autocorrelation test. In essence, these requirements are a test of how well a bit sequence: has zeros and ones equally often; after a sequence of n zeros (or ones), the next bit a one (or zero) with probability one-half; and any selected subsequence contains no information about the next element(s) in the sequence.
• K3 – It should be impossible for any attacker (for all practical purposes) to calculate, or otherwise guess, from any given subsequence, any previous or future values in the sequence, nor any inner state of the generator.
• K4 – It should be impossible, for all practical purposes, for an attacker to calculate, or guess from an inner state of the generator, any previous numbers in the sequence or any previous inner generator states.

For cryptographic applications, only generators meeting the K3 or K4 standard are acceptable.

Mathematical definition[edit]

Given

• ${\displaystyle P}$ – a probability distribution on ${\displaystyle \left(\mathbb{R},\mathfrak{B}\right)}$ (where ${\displaystyle \mathfrak{B}}$ is the standard Borel set on the real line)
• ${\displaystyle \mathfrak{F}}$ – a non-empty collection of Borel sets ${\displaystyle \mathfrak{F}\subseteq \mathfrak{B}}$, e.g. ${\displaystyle \mathfrak{F}=\left\{\left(-\mathrm{\infty },t\right]:t\in \mathbb{R}\right\}}$. If ${\displaystyle \mathfrak{F}}$ is not specified, it may be either ${\displaystyle \mathfrak{B}}$ or ${\displaystyle \left\{\left(-\mathrm{\infty },t\right]:t\in \mathbb{R}\right\}}$, depending on context.
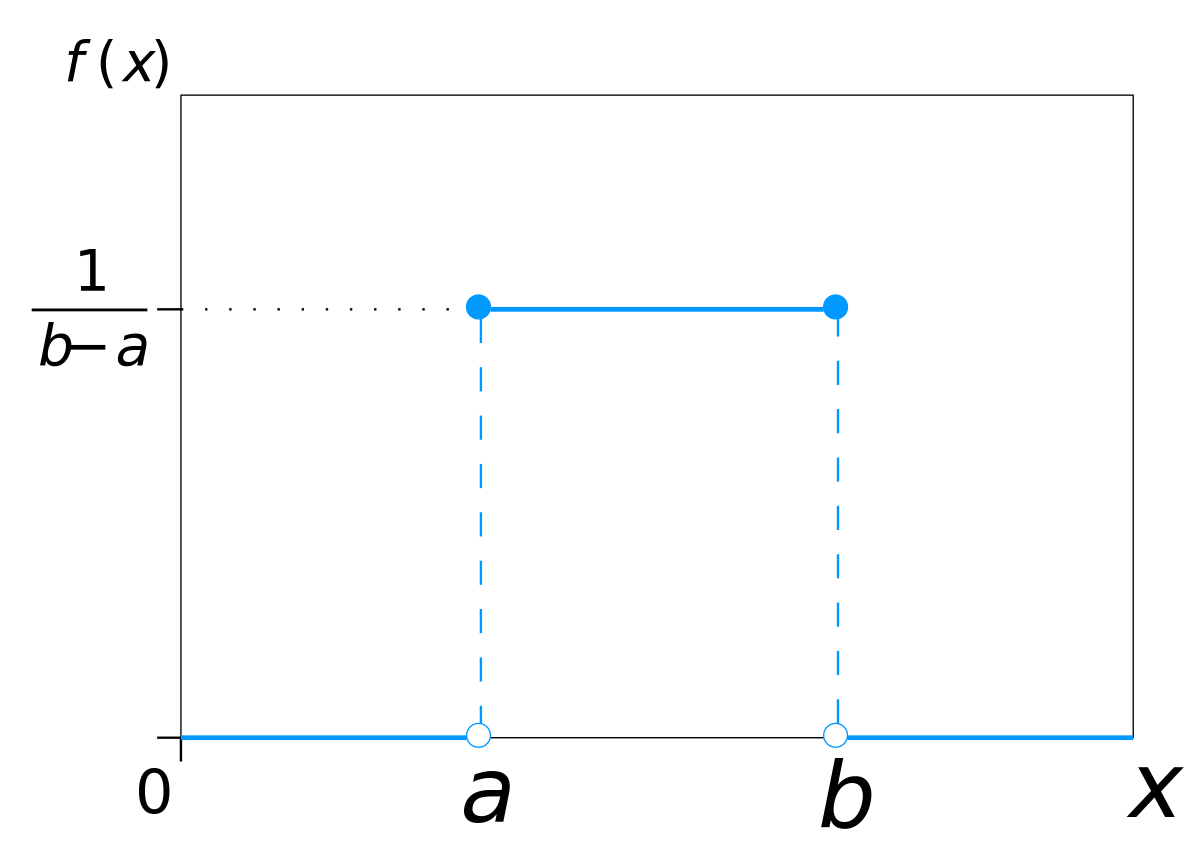
• ${\displaystyle A\subseteq \mathbb{R}}$ – a non-empty set (not necessarily a Borel set). Often ${\displaystyle A}$ is a set between ${\displaystyle P}$'s support and its interior; for instance, if ${\displaystyle P}$ is the uniform distribution on the interval ${\displaystyle \left(0,1\right]}$, ${\displaystyle A}$ might be ${\displaystyle \left(0,1\right]}$. If ${\displaystyle A}$ is not specified, it is assumed to be some set contained in the support of ${\displaystyle P}$ and containing its interior, depending on context.

We call a function ${\displaystyle f:{\mathbb{N}}_1\to \mathbb{R}}$ (where ${\displaystyle {\mathbb{N}}_1=\left\{1,2,3,\dots \right\}}$ is the set of positive integers) a pseudo-random number generator for ${\displaystyle P}$ given ${\displaystyle \mathfrak{F}}$ taking values in ${\displaystyle A}$ iff

• ${\displaystyle f\left({\mathbb{N}}_1\right)\subseteq A}$

(${\displaystyle \mathrm{\#}S}$ denotes the number of elements in the finite set ${\displaystyle S}$.)

It can be shown that if ${\displaystyle f}$ is a pseudo-random number generator for the uniform distribution on ${\displaystyle \left(0,1\right)}$ and if ${\displaystyle F}$ is the CDF of some given probability distribution ${\displaystyle P}$, then ${\displaystyle F^{\ast }\circ f}$ is a pseudo-random number generator for ${\displaystyle P}$, where ${\displaystyle F^{\ast }:\left(0,1\right)\to \mathbb{R}}$ is the percentile of ${\displaystyle P}$, i.e. ${\displaystyle F^{\ast }(x):=inf\left\{t\in \mathbb{R}:x\le F(t)\right\}}$. Intuitively, an arbitrary distribution can be simulated from a simulation of the standard uniform distribution.

Early approaches[edit]

An early computer-based PRNG, suggested by John von Neumann in 1946, is known as the middle-square method. The algorithm is as follows: take any number, square it, remove the middle digits of the resulting number as the 'random number', then use that number as the seed for the next iteration. For example, squaring the number '1111' yields '1234321', which can be written as '01234321', an 8-digit number being the square of a 4-digit number. This gives '2343' as the 'random' number. Repeating this procedure gives '4896' as the next result, and so on. Von Neumann used 10 digit numbers, but the process was the same.

A problem with the 'middle square' method is that all sequences eventually repeat themselves, some very quickly, such as '0000'. Von Neumann was aware of this, but he found the approach sufficient for his purposes, and was worried that mathematical 'fixes' would simply hide errors rather than remove them.

Von Neumann judged hardware random number generators unsuitable, for, if they did not record the output generated, they could not later be tested for errors. If they did record their output, they would exhaust the limited computer memories then available, and so the computer's ability to read and write numbers. If the numbers were written to cards, they would take very much longer to write and read. On the ENIAC computer he was using, the 'middle square' method generated numbers at a rate some hundred times faster than reading numbers in from punched cards.

The middle-square method has since been supplanted by more elaborate generators.

A recent innovation is to combine the middle square with a Weyl sequence. This method produces high quality output through a long period. See Middle Square Weyl Sequence PRNG.

Non-uniform generators[edit]

Numbers selected from a non-uniform probability distribution can be generated using a uniform distribution PRNG and a function that relates the two distributions.

First, one needs the cumulative distribution function${\displaystyle F(b)}$ of the target distribution ${\displaystyle f(b)}$:

Keygen counter strike 1 anthology 10. Counter-Strike 1 Anthology (PC) pack is bundled with a pack of supremely thrilling set of Valve games that includes Counter-Strike, Counter-Strike: Condition Zero and Official. The game is very good condition and also the serial number is working properly with multiple games in the dvd with all being very good. Buy counter strike 1.6 steam key and receive instantly after your payment. Counter-Strike 1.6 (also known as Half-Life: Counter-Strike) is a first-person shooter video game developed by Valve Corporation. It was initially developed and released as a Half-Life modification by - Topic Counter Strike 1.6 Serial Number 2017 + Key (Keygen, License, CD Key) Generator and Activat.

Note that ${\displaystyle 0=F(-\mathrm{\infty })\le F(b)\le F(\mathrm{\infty })=1}$. Using a random number c from a uniform distribution as the probability density to 'pass by', we get

${\displaystyle F(b)=c}$

so that

${\displaystyle b=F^{-1}(c)}$

is a number randomly selected from distribution ${\displaystyle f(b)}$.

For example, the inverse of cumulative Gaussian distribution${\displaystyle {\mathrm{erf}}^{-1}(x)}$ with an ideal uniform PRNG with range (0, 1) as input ${\displaystyle x}$ would produce a sequence of (positive only) values with a Gaussian distribution; however

• When using practical number representations, the infinite 'tails' of the distribution have to be truncated to finite values.
• Repetitive recalculation of ${\displaystyle {\mathrm{erf}}^{-1}(x)}$ should be reduced by means such as ziggurat algorithm for faster generation.

Similar considerations apply to generating other non-uniform distributions such as Rayleigh and Poisson.

See also[edit]

References[edit]

1. ^Barker, Elaine; Barker, William; Burr, William; Polk, William; Smid, Miles (July 2012). 'Recommendation for Key Management'(PDF). NIST Special Publication 800-57. NIST. Retrieved 19 August 2013.
2. ^'Pseudorandom number generators'. Khan Academy. Retrieved 2016-01-11.
3. ^Von Neumann, John (1951). 'Various techniques used in connection with random digits'(PDF). National Bureau of Standards Applied Mathematics Series. 12: 36–38.
4. ^Press et al. (2007), chap.7
5. ^L'Ecuyer, Pierre (2010). 'Uniform random number generators'. In Lovric, Miodrag (ed.). International Encyclopedia of Statistical Science. Springer. p. 1629. ISBN3-642-04897-8.
6. ^Random (Java Platform SE 8), Java Platform Standard Edition 8 Documentation.
7. ^Random.java at OpenJDK.
8. ^Press et al. (2007) §7.1
9. ^Matsumoto, Makoto; Nishimura, Takuji (1998). 'Mersenne twister: a 623-dimensionally equi-distributed uniform pseudo-random number generator'(PDF). ACM Transactions on Modeling and Computer Simulation. ACM. 8 (1): 3–30. doi:10.1145/272991.272995.
10. ^Marsaglia, George (July 2003). 'Xorshift RNGs'. Journal of Statistical Software. 8 (14).
11. ^S.Vigna. 'xorshift*/xorshift+ generators and the PRNG shootout'.
12. ^Vigna S. (2016), 'An experimental exploration of Marsaglia’s xorshift generators', ACM Transactions on Mathematical Software, 42; doi:10.1145/2845077.
13. ^Vigna S. (2017), 'Further scramblings of Marsaglia’s xorshift generators', Journal of Computational and Applied Mathematics, 315; doi:10.1016/j.cam.2016.11.006.
14. ^Panneton, François; L'Ecuyer, Pierre; Matsumoto, Makoto (2006). 'Improved long-period generators based on linear recurrences modulo 2'(PDF). ACM Transactions on Mathematical Software. 32 (1): 1–16. doi:10.1145/1132973.1132974.
15. ^Song Y. Yan. Cryptanalytic Attacks on RSA. Springer, 2007. p. 73. ISBN978-0-387-48741-0.
16. ^Niels Ferguson, Bruce Schneier, Tadayoshi Kohno (2010). 'Cryptography Engineering: Design Principles and Practical Applications, Chapter 9.4: The Generator'(PDF).CS1 maint: Multiple names: authors list (link)
17. ^Klaus Pommerening (2016). 'IV.4 Perfect Random Generators'. Cryptology. uni-mainz.de. Retrieved 2017-11-12. The MICALI-SCHNORR generator
18. ^Pass, Rafael. 'Lecture 11: The Goldreich-Levin Theorem'(PDF). COM S 687 Introduction to Cryptography. Retrieved 20 July 2016.
19. ^Matthew Green. 'The Many Flaws of Dual_EC_DRBG'.
20. ^Katz, Jonathan; Yehuda, Lindell (2014). Introduction to modern cryptography. CRC press. p. 70.
21. ^ ^abSchindler, Werner (2 December 1999). 'Functionality Classes and Evaluation Methodology for Deterministic Random Number Generators'(PDF). Anwendungshinweise und Interpretationen (AIS). Bundesamt für Sicherheit in der Informationstechnik. pp. 5–11. Retrieved 19 August 2013.
22. ^'Security requirements for cryptographic modules'. FIPS. NIST. 1994-01-11. p. 4.11.1 Power–Up Tests. Archived from the original on May 27, 2013. Retrieved 19 August 2013.

Bibliography[edit]

• Barker E., Kelsey J., Recommendation for Random Number Generation Using Deterministic Random Bit Generators, NIST SP800-90A, January 2012
• Brent R.P., 'Some long-period random number generators using shifts and xors', ANZIAM Journal, 2007; 48:C188–C202
• Gentle J.E. (2003), Random Number Generation and Monte Carlo Methods, Springer.
• Hörmann W., Leydold J., Derflinger G. (2004, 2011), Automatic Nonuniform Random Variate Generation, Springer-Verlag.
• Knuth D.E. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN0-201-89684-2. Chapter 3. [Extensive coverage of statistical tests for non-randomness.]
• Luby M., Pseudorandomness and Cryptographic Applications, Princeton Univ Press, 1996. ISBN9780691025469
• von Neumann J., 'Various techniques used in connection with random digits,' in A.S. Householder, G.E. Forsythe, and H.H. Germond, eds., Monte Carlo Method, National Bureau of Standards Applied Mathematics Series, 12 (Washington, D.C.: U.S. Government Printing Office, 1951): 36-38.
• Peterson, Ivars (1997). The Jungles of Randomness : a mathematical safari. New York: John Wiley & Sons. ISBN0-471-16449-6.
• Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P. (2007), Numerical Recipes (Cambridge University Press).
• Viega J., 'Practical Random Number Generation in Software', in Proc. 19th Annual Computer Security Applications Conference, Dec. 2003.

External links[edit]

• TestU01: A free, state-of-the-art (GPL) C++ Random Number Test Suite.
• DieHarder: A free (GPL) C Random Number Test Suite.
• 'Generating random numbers' (in embedded systems) by Eric Uner (2004)
• 'Analysis of the Linux Random Number Generator' by Zvi Gutterman, Benny Pinkas, and Tzachy Reinman (2006)
• 'Better pseudorandom generators' by Parikshit Gopalan, Raghu Meka, Omer Reingold, Luca Trevisan, and Salil Vadhan (Microsoft Research, 2012)
• rand() Considered Harmful on YouTube by Stephan Lavavej (Microsoft, 2013)

Can you tell me any ways to generate non-uniform random numbers?
I am using Java but the code examples can be in whatever you want.

One way is to create a skewed distribution by adding two uniform random numbers together (i.e. rolling 2 dice).

closed as too broad by Bhargav Rao♦May 10 at 7:55

Please edit the question to limit it to a specific problem with enough detail to identify an adequate answer. Avoid asking multiple distinct questions at once. See the How to Ask page for help clarifying this question. If this question can be reworded to fit the rules in the help center, please edit the question.

3 Answers

What distribution of deviates do you want?

Here is a technique which always works, but isn't always the most efficient. The cumulative distrubtion function P(x) gives the fraction of the time that values fall below x. Thus P(x)=0 at the lowest possible value of x and P(x)=1 at the highest possible value of x. Every distribution has a unique CDF, which encodes all the properties of the distrubtion in the way that P(x) rises from 0 to 1. If y is a uniform deviate on the interval [0,1], then x satisfying P(x)=y will be disributed according to your distribution. To make this work comuptationally, you just need a way computing the inverse of P(x) for your distribution.

The Meta.Numerics library defines a large number of commonly used distrubtions (e.g. normal, lognormal, exponential, chi squared, etc.) and has functions for computing the CDF (Distribution.LeftProbability) and the inverse CDF (Distribution.InverseLeftProbability) of each.

For specialized techniques that are fast for particular distrubtions, e.g. the Box-Muller technique for normaly distributed deviates, see the book Numerical Recipies.

Try generating uniformly distributed random numbers, then applying your inverted non-uniform cumulative distribution function to each of them.

If you are using Java then my Uncommons Maths library may be of interest. It includes classes for generating random numbers for Uniform, Gaussian, Poisson, Binomial and Exponential distributions. This article shows how you might use these distributions.

The Complexity Of Nonuniform Random Number Generation Pdf Reader Pdf

Not the answer you're looking for? Browse other questions tagged artificial-intelligencerandom or ask your own question.